首页科技快讯有效复杂性的边界：在有序与无序之间

有效复杂性的边界：在有序与无序之间

来源：晰数塔互联网快讯时间：2025年08月19日 18:13

本文来自微信公众号：集智俱乐部（ID：swarma_org），编辑：赵思怡，作者：Murray Gell-Mann

摘要

本文以讨论复杂性的度量为主线，贯穿了对有效复杂性、规律、复杂适应系统、复杂性的本质与演化等议题的思考。作者认为较高的有效复杂性存在于既非全然有序又非全然无序的事物中。研究对象的有效复杂性可用其所具规律的简洁描述的算法信息量来度量。其中，规律可用计算互算法信息量的方法求得。而复杂适应系统（如生物或生成策略的计算机程序）则决定了研究对象的哪些规律需要被识别。宇宙的基本规律和初始条件都相对简单，有效复杂性主要来源于量子力学所引入的不确定性以及经典物理中混沌现象所带来的不确定性。自组织机制将一些偶然事件转化为“冻结的偶然事件”，而后者会在宇宙的某个粗粒化历史的各部分或各方面之间产生大量的互算法信息，从而形成规律。我们的宇宙从诞生以来，复杂性的外延一直在扩展，但在遥远的未来，复杂性的范围终将萎缩。

集智俱乐部联合北京师范大学教授张江、中国人民大学博士研究生陈绎安、北京师范大学博士研究生陶如意，邱仲普、清华大学博士后刘家臻共同发起「圣塔菲·复杂科学经典论文研读·第一季」读书会，聚焦圣塔菲研究所发布的文集《Foundational Papers in Complexity Science》，这本文集收录了20世纪复杂科学领域89篇重要文献，涵盖熵、演化与适应、非线性动力学与计算等关键主题。读书会自2025年8月22日开始，本周五晚上7:30-9:00，邀请您来参与第一期分享：“走近圣塔菲，我与圣塔菲的故事”。

关键词：有效复杂性、规律、复杂适应系统、互算法信息量、冻结的偶然事件

Murray Gell-Mann丨作者

许宁、罗翠丨翻译

论文题目：What is Complexity?

论文地址：https://complexity.martinsewell.com/Gell95.pdf

复杂性是什么？已有许多的量被提出用于作为诸如复杂性这样的概念的度量。事实上，要全面涵盖我们对于复杂性及其对立面——简单性的所有直观想法，需要多元化的度量。

有些量属于时间（或空间）的度量范畴，例如计算复杂度。这些量关心一台标准通用计算机执行特定任务所需的最短时间（或最小存储空间）。计算复杂度本身即与完成特定计算所需的最少时间（或运行步数）直接相关。

其它被提议的量则属于信息度量范畴，大体而言，它们特指传递特定信息所需的最短消息长度。例如，一个比特串的算法信息量（AIC，algorithmic information content）被定义为使标准通用计算机输出该比特串然后停止运行的最短程序的长度。

所有这样的量，在用于度量现实世界实体的复杂性时，在某种程度上都具有语境相关性甚至主观性。它们依赖对实体的描述的粗粒化程度（即细节的层级）、所假定的对世界已有的知识和理解、使用的语言、从该语言转换为比特串的编码方法，以及对特定理想计算机标准的选择。然而，若研究者考察一系列规模与复杂性递增的相似实体，且仅对规模增大时的度量变化感兴趣，那么很多随机特征自然可以忽略不计。计算复杂度的研究者通常关注当问题规模不断增大时，其求解时间是否随着问题规模的增大呈多项式（而非指数甚或更糟糕的形式）递增。可以说，任何对复杂性的度量最好的用武之地是去比较那些至少有一方在该度量下具有高复杂性的事物。

许多备选量是不可计算的。例如，一个长比特串的AIC很容易被判断为小于或等于某个值。但对任意一个这样的值，都无法排除AIC因该字符串所隐藏的规律（regulaity）被某个尚未发现的定理揭示，从而降到更低的可能性。一个不可压缩比特串则不存在这种规律。这样的比特串被定义为“随机比特串”。一个给定长度的随机比特串拥有最大的AIC，因为能让标准计算机输出它后停止的最短程序，只是一条在该字符串之前加上“PRINT”的指令。

AIC的这种特性，有时也被称为“算法随机性”。这种特性导致其并不适合作为复杂性的度量，否则莎士比亚作品反而比谚语中“由一屋子猴子”随机敲出的相同长度的乱码具有更低的AIC。

能够更好地反映日常对话和科学论述中所提及的“复杂性”的度量，并不是对实体最简描述的长度（大致如同AIC），而是对该实体的规律的集合的简洁描述的长度。因此，一个几乎完全随机、不具备规律的事物，其有效复杂性（effective complexity）接近于零；而一个完全规律的事物，例如一条全由0组成的比特串，其有效复杂性同样也接近于零。只有在完全有序和完全无序之间的中间地带，才存在较高的有效复杂性。

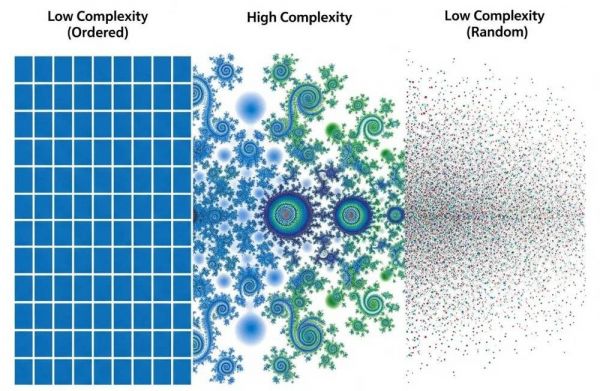
“只有在完全有序和完全无序之间的中间地带，才存在较高的有效复杂性”（图片由AI生成）

没有任何程序可以找出关于实体的所有规律，但这些规律的类别能被识别。发现规律的过程如下：在获取关于实体的可用数据后，将其处理成如比特串的某种形式，然后以特定方式将该串分割成若干部分，并寻找各部分间的互算法信息量（mutural AIC）。例如对于一个被分成两部分的比特串，它的互算法信息量即为各部分AIC之和减去整体的AIC所得的差。超过特定阈值的AIC可被视为出现规律的判定依据。对于已识别的规律，对其所作的描述的AIC即为与之对应的有效复杂性。更准确地说，任何特定的规律都可以被视为将所研究的实体嵌入一个共享这些规律、仅在其他方面有所差异的实体集合中。通常，这些规律会为集合中的每个实体赋予一个概率。（在许多情况下，各实体的概率相同，但不排除实体间概率相异的情况出现。）这些规律的有效复杂性则可定义为描述该实体集合及其概率分布的AIC。（如需详述特定实体，如原始实体，则需要额外信息。）

一些作者试图通过互算法信息(mutual algorithmic information)，而非相应规律的简洁描述的长度来刻画复杂性。然而，这种度量的选择与“复杂性”的一般含义并不怎么相符。举一个简单的例子，任何一个完全由00对和11对组成的比特串，都有着一个显而易见并能用非常简短的方式进行描述的规律，即由奇数位组成的序列与由偶数位组成的序列完全相同。然而，对于一个长比特串而言，这些序列之间的互算法信息量是巨大的。显然，这种情况下，用简短描述的长度来表征复杂性，比用互算法信息量之多寡来表示更为恰当。

既然不可能找出某一实体的所有规律，那么问题就出现了：由谁或由什么来决定哪些类别的规律需要被识别？答案之一指向一类极其重要的系统，其中的每一个系统都在识别到达它的数据流中的特定规律，并将这些规律压缩成一个简洁的信息集。数据流包含了关于系统自身、其所处环境、以及环境与系统行为之间相互作用的信息。这个信息集或“图式（schema）”会经历变化，不同图式之间还会存在竞争。每个图式都可以与部分数据一起被用于描述系统及其所处的环境、预测未来以及为系统设定行为规范。但这种描述和预测可以与更多数据进行比对检验，对比后的反馈会影响图式之间的竞争。同样，符合规范的行为会对现实世界产生实际影响，因而这也会影响竞争。通过这种方式，图式不断演化。其演化总体趋向于作出更好的描述和预测，以及或多或少地顺应现实世界的选择压力。

复杂适应系统（complex adaptive systems）在地球上运作的实例包括：生物进化、动物（包括人类）的学习与思考、哺乳动物及其他脊椎动物的免疫系统功能、人类科学事业的运作、以及那些被设计或编程以生成策略（例如通过神经网络或遗传算法）的计算机的行为。显然，复杂适应系统具有催生其他复杂适应系统的倾向。

复杂适应系统与环境数据交互，生成图式（图片由AI生成）

值得向本刊读者说明的是，例如约翰·霍兰（John Holland）就使用了一套不同的术语来描述一些相同的想法。他用“适应主体（adaptive agent）”来指称上面定义的复杂自适应系统，而用“复杂适应系统”来指称由许多可对彼此行为做出预测的自适应主体组成的复合复杂适应系统（composite complex adaptive system）（如经济或生态系统）。我所说的图式，他称为本质模型（internalmodel）。我们俩都遵从一句老话：科学家宁可用别人的牙刷，也不会用另一位科学家提倡的术语。

当然，任何复杂适应系统在发现规律时都可能犯错。容易迷信、并且经常否认显而易见的事物的我们（人类）对这类错误再熟悉不过了。

除了出错的可能性，我们还应考虑计算难度。从一个高度压缩的图式（例如一个科学理论）和一些特定的附加数据（例如边界条件）中推导出实际的预测结果，需要花费多少时间？在这里，我们就遇到了“复杂性”的时间度量。以逻辑深度为例。对于一个比特串来说，逻辑深度（logical depth）与用标准通用计算机计算该比特串、将其打印出来并停止运行所需的时间有关。这个时间通过对能够完成该任务的各种程序求均值得到。求均值时，较短的程序被给予更大的权重。那么，如果能将实体的适当粗粒化的描述编码成比特串，我们就可以探讨任何实体的逻辑深度。

逻辑深度的一个逆向概念是隐秘度（crypticity），它衡量的是计算机从比特串反推生成它的较短程序之一所需的时间。在人类的科学事业中，我们可以将隐秘度大致理解为从一组数据中构建一个好理论的难度，而逻辑深度则是对从理论出发进行预测的难度的粗略衡量。

通常很难判断一个看起来复杂的事物是真正具有很高的有效复杂性，还是仅仅反映其内在的简单性以及一定程度的逻辑深度的组合。例如，当我们看到曼德尔布罗特著名的分形集的一个相当详细的图案时，在我们了解到它其实可以通过一个非常简单的公式生成之前，我们可能会认为它具有很高的有效复杂性。

它具有的是（甚至并不巨大的）逻辑深度而非有效复杂性。在思考自然现象时，我们经常需要区分有效复杂性和逻辑深度。例如，原子核能级的看似复杂的模式可能很容易被错误地归因于基本层面上的某种复杂定律，但现在人们相信它遵循一个关于夸克、胶子和光子的简单的基础理论，尽管需要大量的计算才能从基本方程推导出其详细模式。因此，这种模式具有相当大的逻辑深度，而有效复杂性却非常低。

现在看来，宇宙中所有物质行为的基本规律，即所有基本粒子及其相互作用的统一量子场论，很可能是非常简单的。(事实上，我们已经有了超弦理论这个貌似合理的候选理论。）同样，描述宇宙在其膨胀之初的初始状态的边界条件可能也很简单。如果这两个命题都是真的，那么是否意味着宇宙中几乎不存在任何有效复杂性？完全不是，因为偶然性在持续不断地起作用。

即便给定了基本规律和初始条件，宇宙的历史也绝非注定。因为这规律是量子力学的，它只能给出各种历史版本的概率。此外，历史只有被充分地粗粒化以显示退相干时（即它们之间没有干涉项）才能被赋予概率值。因此，量子力学带来了大量不确定性，远远超出与海森堡不确定性原理相关的、微不足道的不确定性。

当然，在许多情况下，量子力学概率非常接近确定性，因此确定性的经典物理学是一个很好的近似。但即便在经典条件下，即使规律和初始条件都被精确指定，不确定性仍然可能因为对先前历史的无知而被引入。进而，这种无知的影响可能会被非线性动力学中的混沌现象所放大。在混沌现象中，未来的结果对当前条件的微小变化极其敏感。

我们可以将宇宙可能存在的各种粗粒化历史想象为形成一颗具有分支的树，每个分支都有相应的概率。注意这些是先验概率（priori probability）而非统计概率（statistical probability），除非我们将我们的宇宙视为由许多宇宙构成的巨大集合中的一员，从而形成一个"多重宇宙"。当然，即使在单一宇宙中，也会出现可重复事件（如物理实验）。对于这些事件，这个宇宙的量子力学的先验概率会产生传统的统计概率。

我们周围世界中的任何实体，例如每个人类个体，其存在不仅依赖于简单的基本物理定律和早期宇宙的边界条件，也取决于一连串长得不可思议的概率性事件的结果，而其中每一个事件原本都可能以不同的方式发生。

现在，许多偶然事件，例如气体中某个特定分子在分子碰撞中向右而非向左反弹，在绝大多数情况下对未来的粗粒化历史几乎没有什么影响。然而，有时一个偶然事件可能会对未来产生广泛的影响，尽管这些影响通常局限于特定的时空区域。这种“冻结的偶然事件（frozen accident）”会在宇宙的某个未来的粗粒化历史的各个部分或各方面之间产生大量的互算法信息，对于许多此类历史及其各种划分方式也是如此。

但是，这种产生大量互算法信息的情况，与我们已说到的规律完全相符。因此，随着宇宙历史中时间的推移以及事件（伴随着各种结果的概率）的不断积累，冻结的偶然事件也随之积累，从而产生规律。

宇宙的大部分有效复杂性体现在对那些冻结的偶然事件及其后果的描述的AIC，而只有一小部分来自宇宙的简单的基本定律（基本粒子定律和膨胀开始时的条件）。当然，对于宇宙中的给定实体而言，只有那些造成其自身规律的冻结的偶然事件，才会与基本定律一起，对其有效复杂性有贡献。

随着宇宙变得更加古老，冻结的偶然事件不断堆积，使有效复杂性增加的机会也持续积累。因此，复杂性外延呈扩张趋势，尽管任何给定实体在给定时间段内其复杂性都可能增加或减少。

越来越复杂形式的出现并不是一个仅在复杂适应系统演化中才能见到的现象，尽管对于复杂适应系统而言，在某些特定情况下，增加复杂性可能会带来演化优势。

热力学第二定律要求平均熵（或无序度）增加，但这并不妨碍局部的有序通过各种自组织机制产生。这些机制能将偶然事件转变为其冻结状态，从而产生大量的规律。同样，这类机制也并非仅限于复杂适应系统。

不同的实体在发展出更高复杂性方面可能具有不同的潜力。目前在有效复杂性方面与同类事物没有显著区别的某些事物，却会因其未来可能达到的复杂性而变得引人注目。

因此，定义一个新的量——“潜在复杂性（potential complexity）”，作为未来时间的函数至关重要。对未来时间的定义取决于其相对的固定时刻（比如现在）。这个新的量表示实体在未来某时刻的有效复杂性，它是通过对宇宙在现在到未来那个时刻之间的各种粗粒化历史进行加权平均得到。

越来越多复杂形式随着时间推移不断出现的时代可能不会永远持续下去。在极其遥远的未来，如果宇宙中几乎所有原子核都衰变为电子和正电子、中微子和反中微子以及光子，那么以界限分明的个体为特征的时代可能会走向终结。同时，自组织变得稀有，复杂性的范围也会开始萎缩。

作者简介：

莫里·盖尔曼（Murray Gell-Mann，1929—2019），美国物理学家，1964年提出夸克模型，被誉为“夸克之父”，1969年因其对亚原子粒子的分类及相互作用的研究获诺贝尔物理学奖。1984年，盖尔曼成为圣塔菲研究所的联合发起人之一。他在1994年的短文《Let’s Call It Plectics》中阐述了圣塔菲研究所的学科方向，之后在1995年出版的著作《夸克和美洲豹》中全面展示了其对基本物理规律与生命涌现现象之间的关系的思考。

「系统科学前沿」系列课程

集智学园联合北师大系统科学学院开设「系统科学前沿」系列课程，以方福康先生系统科学文集为思想基石，汇聚北师大系统科学领域十位教授，系统整合统计物理、生命系统中的智能行为、社会复杂系统建模、人工智能与复杂网络等多个交叉方向，构建一条从微观机制到宏观结构、从理论分析到实际应用的知识脉络。

详情请见：系统科学前沿十讲：理解自然、生命与社会的复杂性